ACM RTK - 1. skupina

V Butalah je začelo primanjkovati elektrike.  Da bi vaščane motiviral k varčevanju z njo, je župan odredil, da bo elektrika za tiste, ki je porabijo veliko, dražja kot za tiste, ki je porabijo manj.  Na koncu meseca pošljejo vsakemu vaščanu račun za elektriko, ki ga izračunajo po naslednjih pravilih:

• Recimo, da je ta vaščan porabil v tem mesecu x sodčkov elektrike (Vsi vemo, da se električno energijo meri v kilovatnih urah, vendar je mestni starešina protestiral, češ da elektrike že ne morejo računati v urah, ker ima mesec za vse vaščane enako ur, pa jo odtlej računajo v sodčkih.) (x bo vedno celo število) in da ima ta mesec d dni.
• Za potrebe izračuna se predpostavi, kot da je vsak dan porabil natanko $x/d$ sodčkov elektrike (ne glede na to, kako je bila v resnici razporejena poraba po mesecu).
• Za vsak dan se določi ceno elektrike takole: prvih 6 sodčkov tisti dan stane po 10 dinarjev vsak; naslednjih 6 sodčkov stane po 11 dinarjev vsak; naslednjih 6 sodčkov stane po 12 dinarjev vsak; naslednjih 6 sodčkov stane po 13 dinarjev vsak; vsa preostala poraba se zaračuna po 18 dinarjev na sodček.
• Ceno na dan potem pomnožimo s številom dni v mesecu (torej d) in tako dobimo znesek, ki ga bo moral ta vaščan ta mesec plačati za elektriko.

Primer: recimo, da ima mesec d = 30 dni in da smo porabili x = 819 sodčkov elektrike.  Povprečna dnevna poraba je torej x/d = 819 / 30 = 27,3 sodčkov. Prvih 6 sodčkov na dan stane po 10 dinarjev, naslednjih 6 po 11, naslednjih 6 po 12, naslednjih 6 po 13, preostalih 3,3 sodčkov na dan (ker je 27,3 - 4 * 6 = 3,3) pa stane po 18 dinarjev.  Cena na dan je torej 6 * 10 + 6 * 11 + 6 * 12 + 6 * 13 + 3,3 * 18 = 335,4 dinarjev, za ves mesec pa $335,4 * d = 10 062 dinarjev.

V praksi porabijo Butalci pozimi več elektrike kot poleti in jo zato v mesecih, ko je porabijo veliko, tudi dražje plačujejo.  Toda Cefizelj se je domislil, da bi lahko prihranil kar nekaj denarja, če bi porabo prerazporedil po mesecih (pri čemer bi skupna poraba ostala enaka).

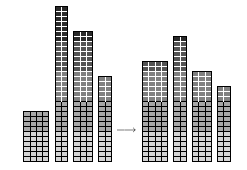
Leva slika kaže primer porabe v štirimesečnem obdobju; sodčki, ki jih plačamo po višji ceni, so predstavljeni s temnejšimi odtenki sive.  Širina stolpcev ponazarja dolžino meseca (v praksi seveda razlike v dolžini mesecev niso tako dramatične kot na naši sliki). Desna slika kaže, kako bi lahko isto skupno porabo razporedili med te štiri mesece tako, da bi bila skupna cena manjša (čeprav ne nujno tudi najmanjša možna).

Napiši program, ki prebere s standardnega vhoda 12 celih števil, ki predstavljajo porabo elektrike po mesecih od januarja do decembra, in

1. izpiše skupno ceno elektrike, ki bi jo v tem letu pri takšni porabi po mesecih plačali; in
2. izpiše, kako bi morali elektriko razporediti po mesecih, da bi bila skupna letna poraba enaka kot v vhodnih podatkih, skupna cena elektrike pa najmanjša možna. Izpiše naj tudi skupno ceno elektrike za celo leto pri tako preprazporejeni porabi. Pri tem pa upoštevaj omejitev, da mora biti mesečna poraba za vsak mesec še vedno celo število sodčkov.  Če je možnih več enako dobrih rešitev, je vseeno, katero izpišeš.

Program, ki reši le podnalogo 1., dobi največ 8 točk (od 20 možnih).  Pri vseh izračunih lahko predpostaviš, da ima februar 28 dni.

<PDF>