ACM RTK - 2. skupina

Tiskana vezja

Ker se Štefko zanima za elektroniko, je za rojstni dan dobil začetniški komplet za izdelavo tiskanih vezij. Paket vsebuje več plošč, ki že imajo narejene luknjice za priključke. Poleg tega je dobil orodje, s katerim lahko med poljubnima dvema luknjicama (priključkoma) nariše ravno (bakreno) povezavo. Luknjice so postavljene na ploščo na tak zvit način, da nobena ravna črta med dvema luknjicama ne prečka katere druge luknjice. Štefko je že pripravil načrte za nekaj genialnih vezij, ko pa jih je hotel narisati, je opazil - ojoj! - da bi se nekatere daljice med seboj sekale, če bi jih zares narisal na ploščo. Ko je vezje načrtoval, je mislil samo na to, kateri pari priključkov morajo biti med seboj povezani.

Ampak ni še vse izgubljeno. Štefko je kmalu opazil, da je plošča dvostranska! Razmišljal je takole: kaj pa, če nekaj povezav narišem na eno, nekaj pa na drugo stran plošče? Potem morda lahko dosežem, da se nobeni dve povezavi ne bosta sekali? Zdaj ga zanima, katera vezja je možno narisati, če lahko uporabi obe strani plošče. Ker je problem za Štefka preveč zapleten, potrebuje tvojo pomoč. Opiši postopek, ki ugotovi, ali je mogoče dano vezje narisati na opisani način, ne da bi se kakšni dve povezavi sekali. Pri tem tvoj postopek kot vhodne podatke dobi koordinate vseh luknjic (luknjice oštevilčimo od 1 do n in recimo, da ima i-ta luknjica koordinate (x_i,y_i)) in seznam parov luknjic, ki jih je treba povezati. Opiši tudi, kako bi v svoji rešitvi predstavil in organiziral te podatke v pomnilniku. Predpostavi, da že obstaja funkcija SeSekata(ax, ay, bx, by, cx, cy, dx, dy), ki vrne true, če se daljica od točke (a_x,a_y) do točke (b_x,b_y) seka z daljico od točke (c_x,c_y) do točke (d_x,d_y), sicer pa vrne false.

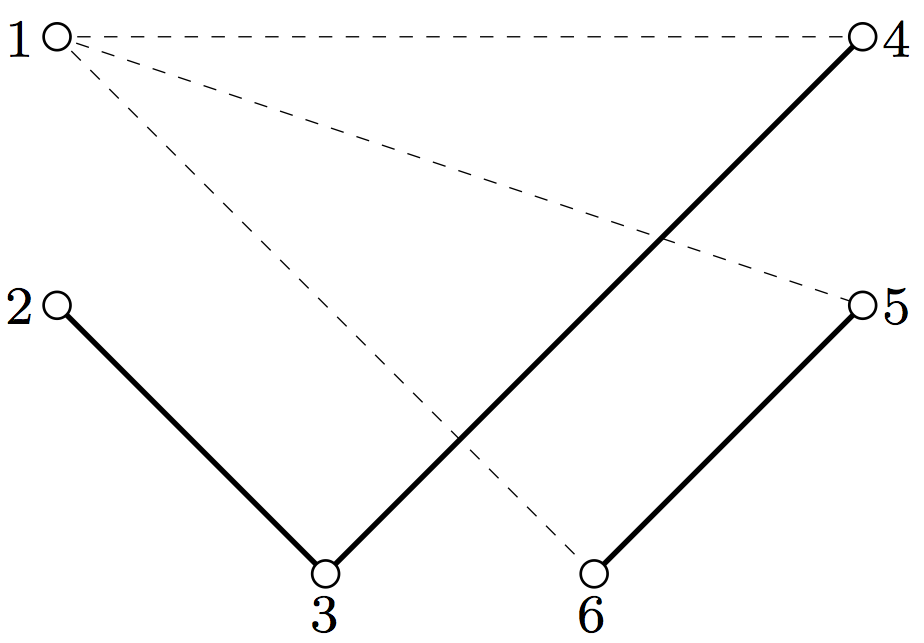
Primer: gornja slika kaže vezje, ki bi se ga dalo narisati na opisani način; pri tem debele polne črte pomenijo povezave na eni strani plošče, tanke črtkane črte pa povezave na drugi strani plošče. Če pa bi hoteli temu vezju dodati še povezavo med luknjicama 2 in 5, se ga ne bi več dalo narisati brez križanja povezav.