ACM RTK - 2. skupina

Strahopetni Hektor

Pojdimo v čas trojanske vojne, ko Ahajci napadajo Trojance, ki čepijo za svojim obzidjem. Zid je zgrajen iz n dolgih kamnitih blokov, visokih 1 enoto, ki so položeni vodoravno drug na drugega, tako da se ne porušijo. Na vsaki višini imamo le en blok; za blok na višini i (za i = 1,2,...,n) je znano, da se začne na x-koordinati z_i in je dolg d_i enot.

Ti si na strani Ahajcev in želiš z ogromnim katapultom porušiti trojansko obzidje; na voljo imaš več krogel, s katerimi lahko ustreliš v zid in razbiješ najbolj levo enoto izbranega bloka. Če uspeš popolnoma uničiti en blok, se zid podre in Hektor, poveljnik trojanske strani, se nemudoma vda (to se zgodi celo, če je uničen vrhnji blok). Vendar je dovolj razbiti kakšen blok tudi le toliko, da se del zidu nad njim prevrne. To se zgodi, ko njegovo težišče ni več podprto s spodnjim blokom. Tudi če se v tem primeru zid le nagne, Hektor in njegova vojska izgubijo vse upanje na zmago in se predajo.

Opiši postopek (ali napiši program, če ti je lažje), ki bo pomagal Ahajcem simulirati potek rušenja takega obzidja, da se bodo lažje pripravili na boj. Postopek na začetku dobi opis zidu (vrednosti n, z₁, ..., z_n in d₁, ..., d_n), nato pa naj v zanki bere podatke o izstreljenih kroglah (za vsako kroglo je podano, v kateri blok je bila izstreljena - to je število od 1 do n, pri čemer 1 pomeni najnižji blok, n pa najvišjega) in po vsaki prebrani krogli takoj sproti (še preden prebere naslednjo kroglo) izpiše, ali zid zdaj še stoji ali je že podrt.

Fizikalni poduk: x-koordinata težišča je definirana kot povprečje x-koordinat posameznih enot zidu. Vse enote zidu so enako težke. Če se težišče nahaja točno nad robom podpore, se telo še ne prevrne.

Primer: recimo, da imamo zid višine n = 6 z naslednjimi začetnimi podatki:

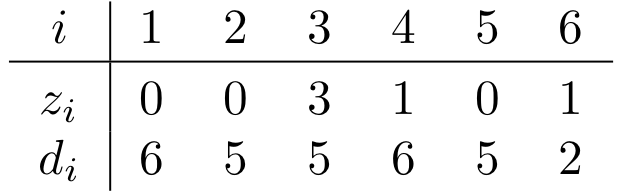
Ahajci bi lahko zid (ne nujno optimalno) napadali takole:

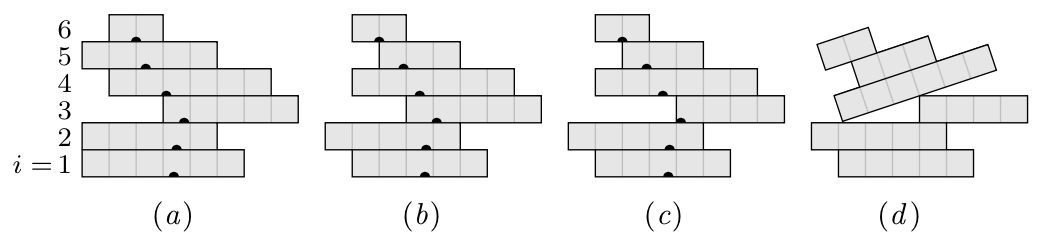
(a) Začetno stanje zidu. Črna pika na spodnjem robu posameznega bloka označuje položaj težišča tistega dela zidu, ki ga sestavljajo ta blok in vsi nad njim. - (b) Stanje zidu po treh strelih, enem na višini 1 in dveh na višini 5. Zid je še vedno stabilen. - (c) Če nato izvedemo še en strel na višini 3, zid ni več stabilen: blok 3 ne podpira več težišča blokov 4, 5, 6. Ti bi se zato nagnili in prevrnili, kot kaže slika (d).