ACM RTK - 2. skupina

Razpolovišče lika

Nekoč je živel kralj, ki je umrl. Kraljestvo je v oporoki zapustil svojima sinovoma — vsakemu natanko polovico. Njegova želja je, da se kraljestvo razdeli na dva dela s popolnoma ravno mejo, ki poteka točno v smeri vzhod–zahod. Dvorni geometri imajo težavo določiti primerno lego meje. Pomagaj jim.

Zemljevid obstoječega kraljestva je znan. Vrisan je na karirasto mrežo širine w in višine h kvadratkov in orientiran tako, da kaže sever navpično navzgor. Na mreži je vsak kvadratek bodisi bel bodisi črn; črni kvadratki sestavljajo kraljestvo.

Napiši podprogram (funkcijo), ki pregleda zemljevid kraljestva in vrne y-koordinato tiste vodoravne črte (premice), za katero sta površini kraljestva pod in nad črto enaki. Če ob razrezu kraljestva »podkraljestvi« razpadeta na več kosov, nas to ne moti. Koordinatni sistem postavimo tako, da ima izhodišče v spodnjem levem vogalu zemljevida, enota pa je enaka stranici enega kvadratka na karirasti mreži. Pozor — iščemo točno vrednost za y in ta ni nujno celoštevilska. (Predpostavi, da so podatkovni tipi, ki jih tvoj programski jezik uporablja za predstavitev realnih števil (npr. float ali double) dovolj natančni za potrebe te naloge, torej ti ni treba skrbeti zaradi morebitnih majhnih zaokrožitvenih napak.)

Nalogo lahko rešiš tudi tako, da izpišeš celoštevilski y, ki čim bolje (čeprav morda ne čisto natančno) razpolovi kraljestvo. Takšne rešitve bodo vredne največ 10 točk (od 20).

Pri pisanju podprograma privzemi, da imaš nekje že definirani spremenljivki w in h, ki hranita širino oz. višino zemljevida (v številu kvadratkov), ter funkcijo Znotraj(x, y), ki vrne 1, če je kvadratek s koordinatama (x, y) na zemljevidu črn, sicer pa 0.

Primer:

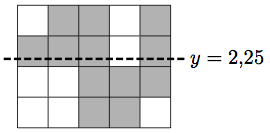
Na sliki je w = 5, h = 4. Vrisana je tudi iskana rešitev — meja poteka na višini y = 2,25. V tem primeru je vrstica razrezana po četrtini in zato južni polovici kraljestva prispeva en kvadratek ploščine, severni polovici pa tri kvadratke. Tako imata severna in južna polovica res enako skupno ploščino, namreč 6 kvadratkov. Rešitev za 10 točk, ki vedno vrača celoštevilske y, pa bi morala pri primeru s slike vrniti y = 2.

PDF besedilo.